חוקי לוגריתמים - log
- 28 ביולי 2024
- זמן קריאה 2 דקות
עודכן: 28 בדצמ׳ 2025
חוקי לוגריתמים - log | חוקי לוגים | לוגריתמים נוסחאות
מהו לוגריתם - log?
לוגריתם הוא בעצם הפעולה ההפוכה לחזקה, והוא משמש לפירוק והבנה של ביטויים מתמטיים מורכבים.
בפוסט זה נלמד מהו log, מהם חוקי הלוגריתמים המרכזיים - חוק המכפלה, חוק המנה וחוק החזקה, והכי חשוב - כיצד משתמשים בהם בפועל, כולל שינוי בסיס ודוגמאות מפורטות.
בואו נתחיל!
לוגריתם עונה על שאלה אחת פשוטה:
לאיזו חזקה צריך להעלות מספר מסוים כדי לקבל מספר אחר?
כלומר, אם אנחנו יודעים את התוצאה ואת הבסיס - הלוגריתם עוזר לנו למצוא את החזקה.
נניח שאנחנו מעלים את המספר b בחזקה מסוימת ומקבלים את המספר a, אז הלוגריתם של a בבסיס b הוא אותה חזקה.
זה כל הסיפור. לוגריתם = חיפוש החזקה.
אם מתקיים:

אז:

ובמילים פשוטות: הלוגריתם אומר לנו מהו x.
בוא נראה את בדוגמה:

ולכן משוואת הלוגריתם שלנו תהיה:
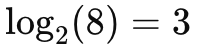
כלומר:
הלוגריתם שואל –
“לאיזו חזקה צריך להעלות 2 כדי לקבל 8?”
והתשובה היא 3.
ערכי לוגריתמים קבועים: לוג של 1 - לא משנה מה הבסיס יהיה שווה אפס. לוג של מספר על בסיס אותו מספר יהיה שווה אחד.

חשוב לזכור: הבסיס חייב להיות מספר חיובי ושונה מ-1
חוק המכפלה:

חוק זה אומר שהלוגריתם של מכפלת שני מספרים שווה לסכום הלוגריתמים של כל אחד מהמספרים.
חוק המנה:

חוק זה אומר שהלוגריתם של מנה בין שני מספרים שווה להפרש בין הלוגריתמים של כל אחד מהמספרים.
חוק החזקה:

חוק זה אומר שהלוגריתם של מספר בחזקה שווה למכפלת החזקה בלוגריתם של המספר.
שינוי בסיס הלוגריתם:
לרוב, במחשבונים ברירת המחדל היא לוגריתם על בסיס 10. אם נרצה לחשב לוגריתם על בסיס שונה, נשתמש בנוסחה לשינוי בסיס:

דוגמאות לשימוש בחוקי הלוגריתמים:
דוגמה למכפלה:

דוגמה למנה:

דוגמה לחזקה:

📄 דף נוסחאות מקצועי - חוקי לוגריתמים
✓ כל החוקים במקום אחד
✓ דוגמאות פתורות צעד אחר צעד
✓ טיפים למבחן
✓ מוכן להדפסה ולשימוש
הורד עכשיו בחינם ↓
סיכום
לוגריתמים יכולים להיות כלי חזק וחשוב לפתרון בעיות במתמטיקה ובמדעים. חשוב להבין את חוקי הלוגריתמים ולהשתמש בהם בצורה נכונה. אם אתם עדיין מתקשים, אתם מוזמנים לפנות למורים הפרטיים של Class-A שילוו אתכם בדרך להצלחה.





תגובות